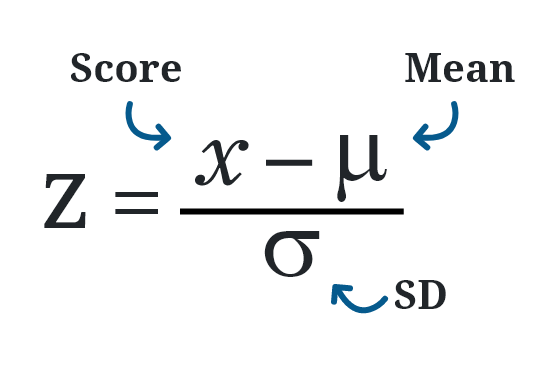Z Score Calculator is a statistical tool that assistances in standardizing data by altering it into a normal distribution. It compares data points from several datasets to create their relative placements. The Z Score calculates the distance between a data point and the dataset's mean in standard deviations.
What is the z-score?
The Z score is a statistic that indicates, in terms of standard deviations, how distant a data point is from the dataset's mean. Thanks to its assistance in standardizing data, we can compare data points across various datasets.
The formula of the z-score:
Calculating the z score needs the following formula:
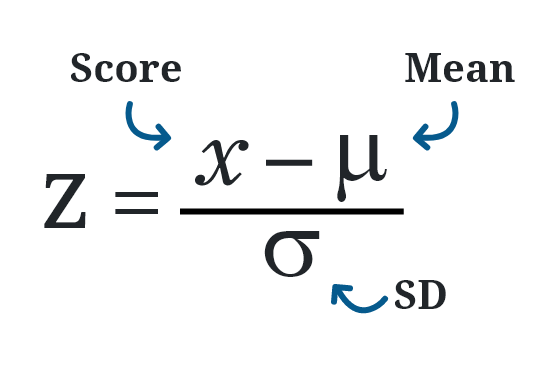
Where:
- The standard score value is Z.
- The data point's value is X.
- The Population mean value is µ.
- The Population Std Dev value is (σ).
Uses of Z-score:
Generally, the z-score is used to measure the deviation value from the mean of the data set We use the Z-score in many fields like finance, engineering, medicine, psychology, etc.
- In finance, it is used to measure the solvency of corporations.
- In engineering, it is used to fix a product's or a process's quality.
- In medicine, it is used to identify conditions such as malnourishment and growth disorders.
- In psychology, it is used to analyze knowledge and academic disabilities.
- It’s used in identifying outliers, testing hypotheses, monitoring processes, and controlling quality.
Example section:
In this section, we’ll solve the example to gain a more complete understanding of this topic.
Example 1:
Find the Z-score value when the sample mean is x̄ = 48, Sample Size n = 12, the population mean μ = 12, and Population Standard deviation (σ) = 8
Solution:
Step 1: Extract the data
x̄ = 48
μ = 12
σ = 8
n = 12
Step 2: Formula
Z = (x̄ - μ) / (σ / √n)
Step 3: Put values in the formula,
Z = (48 - 12) / (8 / √12)
Z = (36 / 2.3094010767585)
Z = 15.58846
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
