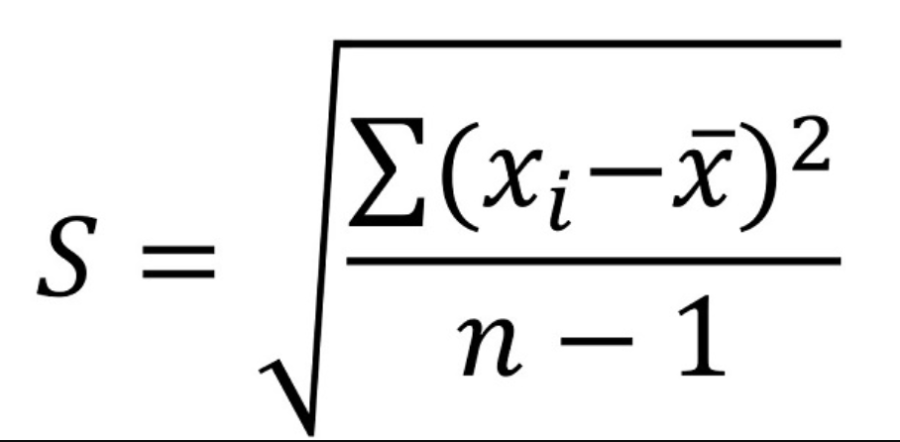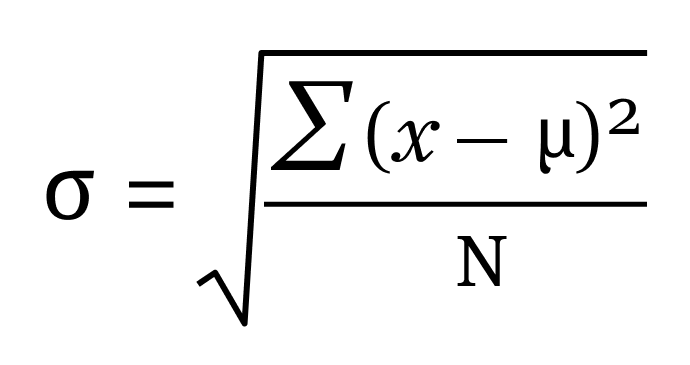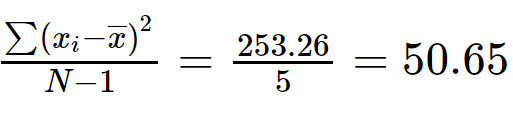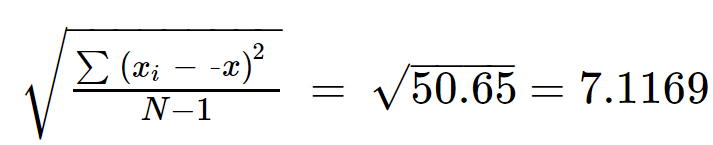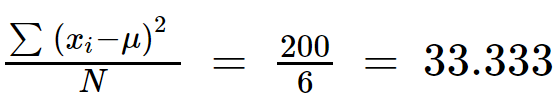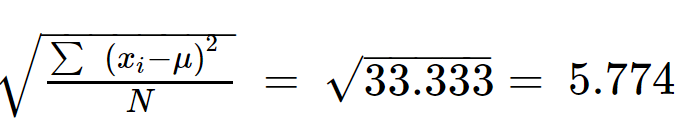Standart sapmanın tanımı, bağıl standart sapma hesaplayıcısı kullanmadan standart sapmanın nasıl bulunacağı ve standart sapma denklemi gibi birkaç önemli noktayı inceleyelim.
Standart sapma nedir?
Sayıların ne ölçüde yayıldığının ölçüsü.
Standart Sapma, bir veri kümesinin ortalamasına göre dağılımını ölçen ve varyansın karekökü olarak hesaplanan bir istatistiktir. Yunan sembolü sigma σ ile gösterilir.
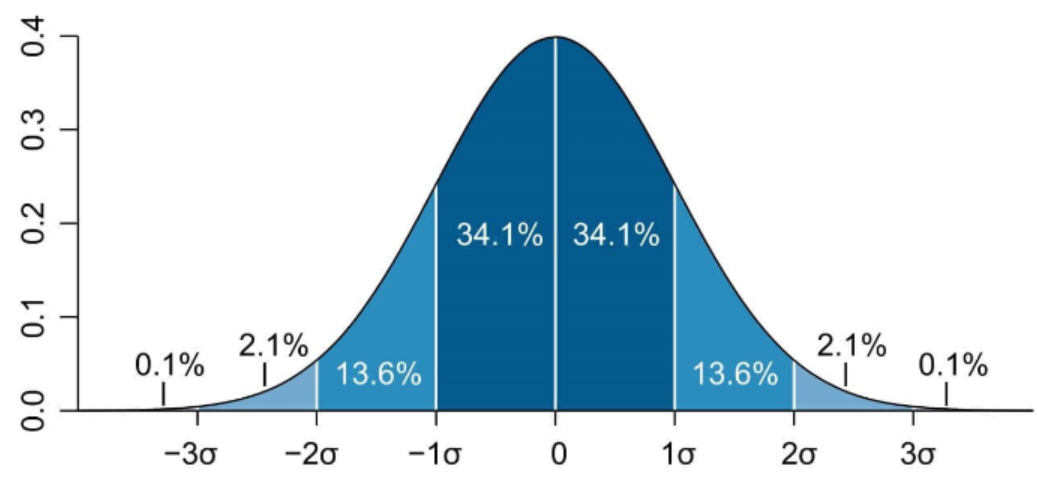
Aşağıda 1 bant genişliğine sahip normal dağılımın grafiğini bulabilirsiniz.
Standart Sapma Formülü
Standart sapma formülü, karekökü alınarak ifade edilebilir. varyans .
Örnek Standart Sapma Formülü
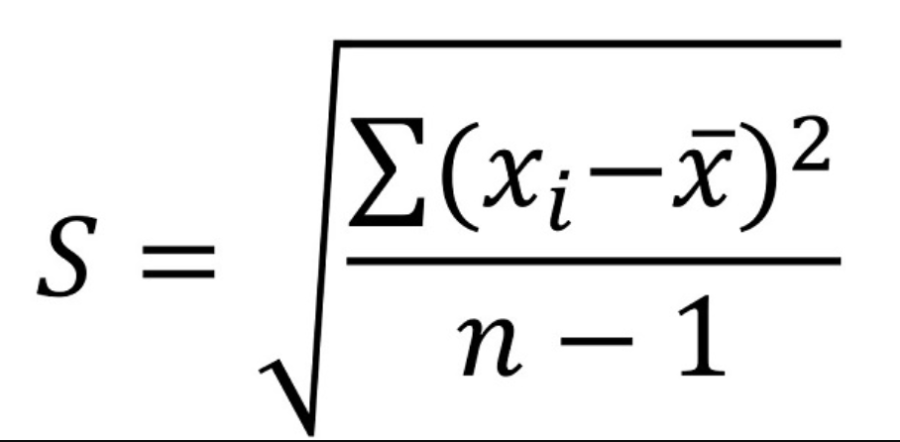
- S örnek standart sapmasını ifade eder
- N gözlem sayısıdır
- X Ben örnek öğenin gözlemlenen değerleridir ve
- X numunenin ortalama değeridir
Nüfus Standart Sapma Formülü
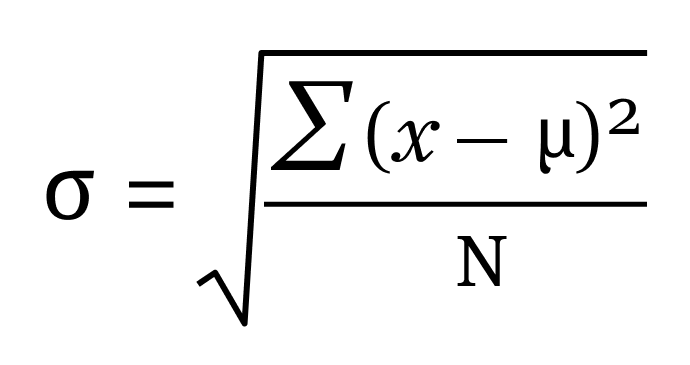
- σ nüfus standart sapmasını ifade eder
- N nüfusun büyüklüğü
- X Ben popülasyonda gözlemlenen değerlerdir ve
- μ nüfus demek mi
Standart Sapma Nasıl Hesaplanır?
Standart sapma hesaplaması yukarıdaki ortalama ve standart sapma hesaplayıcısı kullanılarak yapılabilir. Ancak SD hesaplama yöntemini örneklerle açıklayacağız.
Örnek 1: Örnek Standart Sapma İçin
Verilen örneğin standart sapmasını bulun:
30, 20, 28, 24, 11, 17
Çözüm
Aşama 1: Hesapla Anlam örnek verilerin değeri:
N = 6
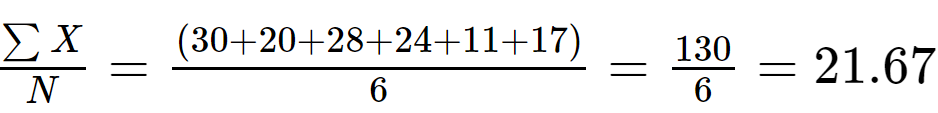
Adım 2: Hesapla (x Ben - x̄) veri setindeki her bir değerden ortalama değeri çıkararak farkların karesini hesaplayarak bunları pozitif hale getirin.
| Veri Değerleri (x Ben ) | X Ben - x̅ | (X Ben - X ) 2 |
| 30 | 30 - 21,67 = 8,33 | (8.332) 2 = 69,4 |
| 20 | 20 - 21,67 = -1.67 | (-1.672) 2 = 2,78 |
| 28 | 28 - 21,67 = 6,33 | (6.332) 2 = 40 |
| 24 | 24 - 21,67 = 2,33 | (2.332) 2 = 5,43 |
| 11 | 11 - 21,67 = -10,67 | (-10.672) 2 = 113,85 |
| 17 | 17 - 21,67 = -4,67 | (-4.672) 2 = 21,80 |
Aşama 3: (x) için tüm değerlerin toplamını alın Ben - X) 2 .
&toplam;(x Ben - X) 2 = 69,4 + 2,78 + 40 + 5,43 + 113,85 + 21,80
&toplam;(x Ben - X) 2 = 253,26
Adım 4: &toplamı böl (x Ben - X) 2 (N-1) ile.
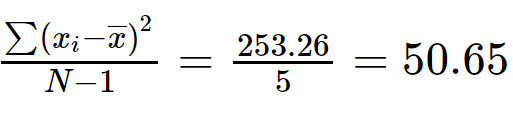
Varyans = 50,65
Adım 5: ∑(x'in karekökünü alın Ben - X) 2 /(N-1) standart sapmayı elde etmek için.
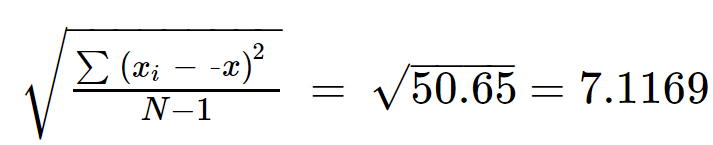
s = 7,1169
Yukarıdaki örnek standart sapma hesaplayıcısı, bu örneğin sonucunu kontrol etmek için kullanılabilir.
Örnek 2: Nüfus İçin Standart sapma
Verilen nüfus verilerinin standart sapmasını bulun:
10, 12, 18, 14, 21, 27
Çözüm
Aşama 1: Nüfus verilerinin beklenen değerini hesaplayın:
N = 6
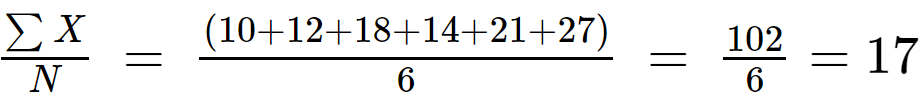
Adım 2: Hesapla (x Ben - µ) veri setinin her bir değerinden ortalama değeri çıkararak ve farklılıkların karesini hesaplayarak bunları pozitif hale getirin.
| Veri Değerleri (x Ben ) | X Ben - &mikro; | (X Ben - &mikro;) 2 |
| 10 | 10 - 17 = -7 | (-7) 2 = 49 |
| 12 | 12 - 17 = -5 | (-5) 2 = 25 |
| 18 | 18 - 17 = 1 | (1) 2 = 1 |
| 14 | 14-17 = -3 | (-3) 2 = 9 |
| 21 | 21 - 17 = 4 | (4) 2 = 16 |
| 27 | 27 - 17 = 10 | (10) 2 = 100 |
Aşama 3: (x) için tüm değerlerin toplamını alın Ben - &mikro;) 2 .
∑ (x Ben - &mikro;) 2 = 49 + 25 + 1 + 9 + 16 + 100
&toplam;(x Ben - M) 2 = 200
Adım 4: &toplamı böl (x Ben - &mikro;) 2 (N) ile.
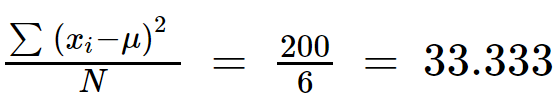
Varyans = 33.333
Adım 5: ∑(x'in karekökünü alın Ben - &mikro;) 2 /N standart sapmayı almak için.
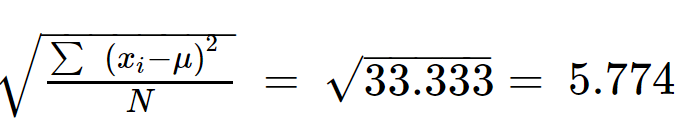
σ = 5,774
SD hesaplamalarına yönelik değerleri çapraz kontrol etmek için yukarıdaki popülasyon standart sapma hesaplayıcısını kullanın.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
