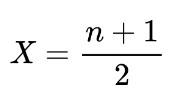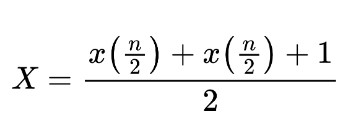Median Calculator
Use the median calculator to find the mid-value of a dataset. Everything required, from the formula to the steps, to calculate the answer is mentioned in the solution.
What is the median?
The Median refers to the value in the center of a presented dataset. The middle-value. It is sometimes a value from the data and other times an average or mean of two values.
Median formula:
There are two formulas for the median. Both are pretty simple. If the data has an odd number of values then:
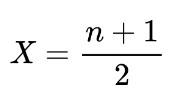
If the data values are in an even number then:
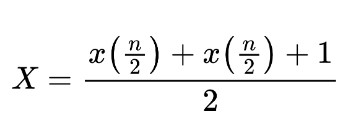
X is the median and n is the total count of values.
How to find the median?
The first step is to arrange the dataset. Use the ascending order. After that, count the number of values and use the suitable formula accordingly.
If it is odd then add one (1) to the total number of values. After that, divide by 2. The resultant value will tell what number of values is the median value.
For an even dataset, divide the total number by two and further add one. Locate the values that are present at the place of the calculated numbers and add them. Lastly, divide by 2.
Example:
What are the medians of these datasets?
- 3 , 11 , 4 , 6 , 8 , 9 , 6
- 10 , 10 , 34 , 23 , 54 , 9
Solution:
For the first data:
Step 1: Arrange the data.
= 3 , 11 , 4 , 6 , 8 , 9 , 6
= 3 , 4 , 6 , 6 , 8 , 9 , 11
Step 2: Calculate the total number of values.
There are a total of 7 values.
Step 3: Use the formula.
X = n + 1 / 2
X = 7 + 1 / 2
X = 8 / 2
X = 4th value
Step 4: locate the value.
The 4th value of arranged data is 6.
For the first data:
Step 1: Arrange the data.
= 10 , 10 , 34 , 23 , 54 , 9
= 9 , 10 , 10 , 23 , 34 , 54
Step 2: Calculate the total number of values.
There are a total of 6 values.
Step 3: Use the formula.
x = n/2 , = n/2 + 1
x = 6 / 2 , = 6/2 + 1
x = 3rd value , = 3 + 1 = 4th value
Step 4: Locate the values.
The 3rd and 4th values of arranged data are 10 and 23.
Step 5: Add and divide by 2.
= 10 + 23
= 33
= 33/2
= 16.5
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
