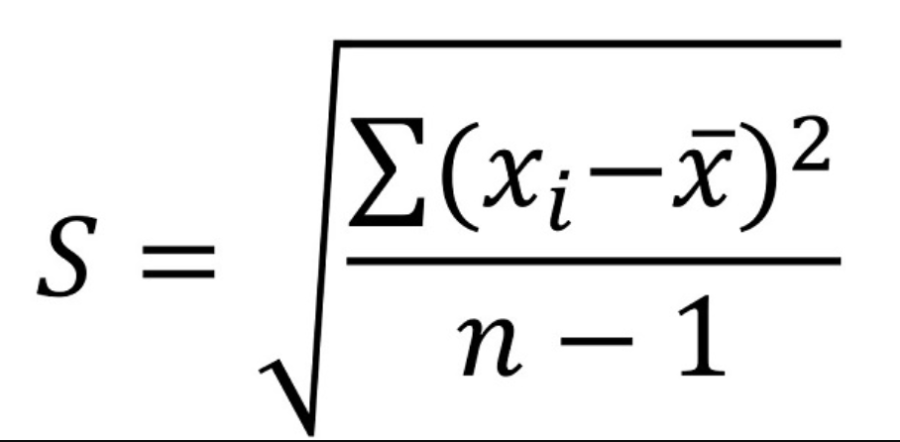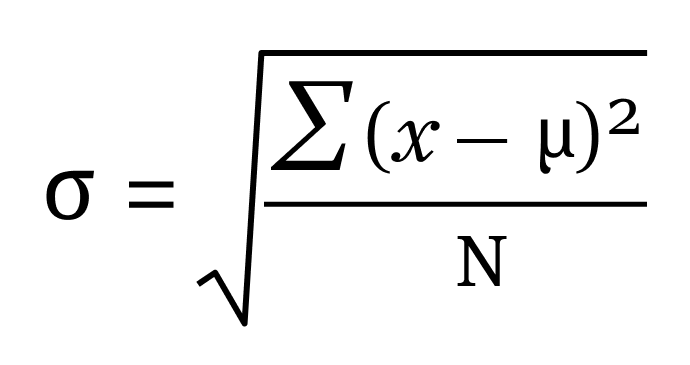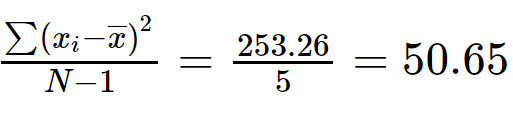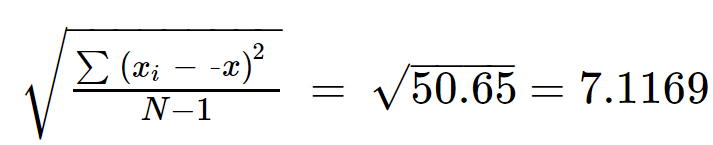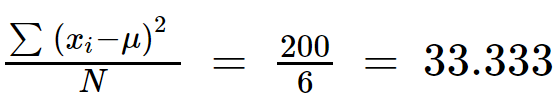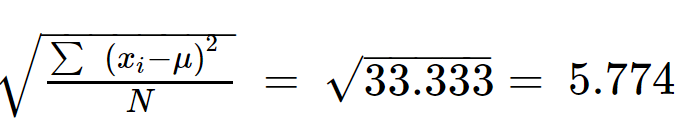표준편차 정의, 상대표준편차 계산기를 사용하지 않고 표준편차를 구하는 방법, 표준편차 방정식 등 몇 가지 핵심 사항을 살펴보겠습니다.
표준편차란 무엇입니까?
숫자가 퍼져 있는 정도를 측정한 것입니다.
표준편차는 평균을 기준으로 데이터 세트의 분산을 측정하는 통계이며 분산의 제곱근으로 계산됩니다. 이는 그리스 기호 시그마 σ로 표시됩니다.
아래에서 폭이 1 밴드인 정규 분포의 플롯을 찾을 수 있습니다.
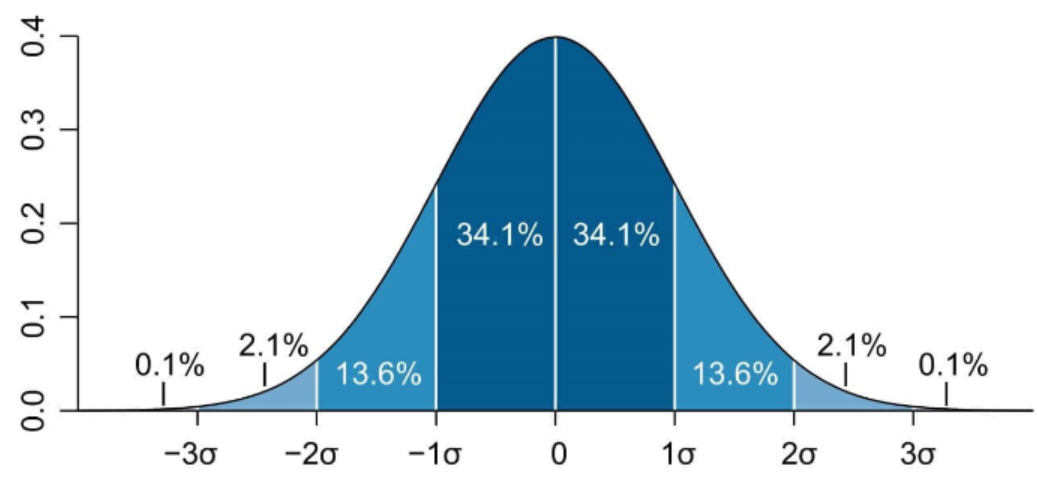
표준편차 공식
표준 편차 공식은 분산의 제곱근을 취함으로써 표현 될 수 있습니다.
샘플 표준편차 공식
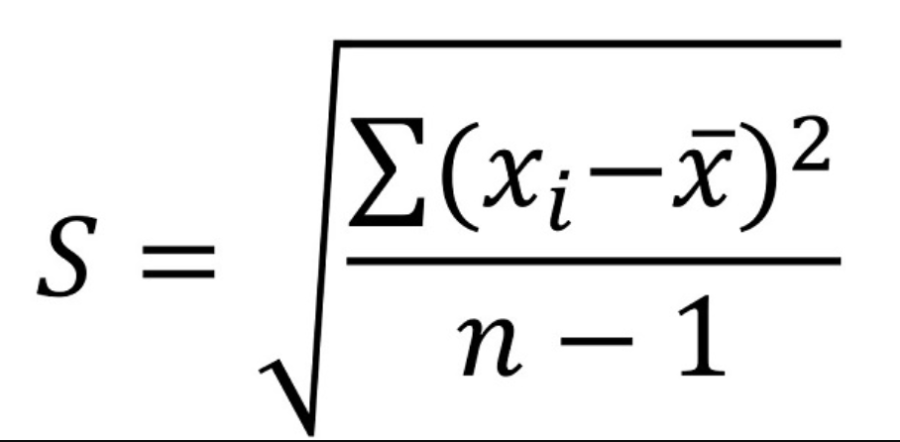
- 에스 표본 표준편차를 나타냅니다.
- N 관측치 수입니다
- 엑스 나 는 샘플 항목의 관측된 값입니다.
- 엑스 표본의 평균값입니다.
모집단 표준편차 공식
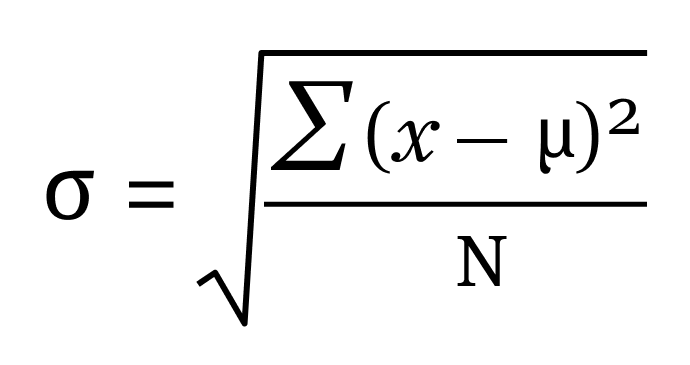
- &시그마; 모집단 표준편차를 의미합니다.
- N 인구의 규모이다
- 엑스 나 는 모집단에서 관측된 값입니다.
- μ; 인구 평균인가
표준편차를 계산하는 방법은 무엇입니까?
표준편차 계산 위의 평균 및 표준편차 계산기를 사용하여 수행할 수 있습니다. 그러나 SD를 계산하는 방법을 예를 들어 설명하겠습니다.
예 1: 표본 표준편차의 경우
주어진 표본의 표준편차를 구합니다:
30, 20, 28, 24, 11, 17
해결책
1 단계: 계산하다 평균 샘플 데이터의 값:
N = 6
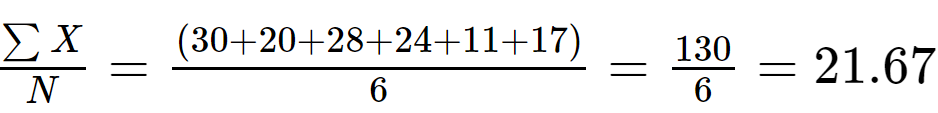
2 단계: 계산 (x 나 - x̄) 데이터 세트의 각 값에서 평균값을 빼고 차이의 제곱을 계산하여 양수로 만듭니다.
| 데이터 값(x 나 ) | 엑스 나 - x̅ | (엑스 나 -x̅) 2 |
| 30 | 30 - 21.67 = 8.33 | (8.332) 2 = 69.4 |
| 20 | 20 - 21.67 = -1.67 | (-1.672) 2 = 2.78 |
| 28 | 28 - 21.67 = 6.33 | (6.332) 2 = 40 |
| 24 | 24 - 21.67 = 2.33 | (2.332) 2 = 5.43 |
| 11 | 11 - 21.67 = -10.67 | (-10.672) 2 = 113.85 |
| 17 | 17 - 21.67 = -4.67 | (-4.672) 2 = 21.80 |
3 단계 : 3 단계 : (x에 대한 모든 값의 합을 구합니다. 나 -x̅) 2 .
=(x 나 -x̅) 2 = 69.4 + 2.78 + 40 + 5.43 + 113.85 + 21.80
=(x 나 -x̅) 2 = 253.26
4단계: 나누기 =(x 나 -x̅) 2 (N-1)과 함께.
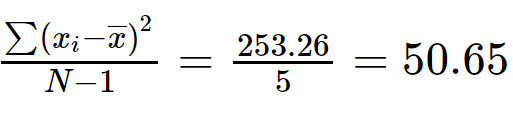
분산 = 50.65
5단계: \(x)의 제곱근을 구합니다. 나 -x̅) 2 /(N-1) 표준편차를 구합니다.
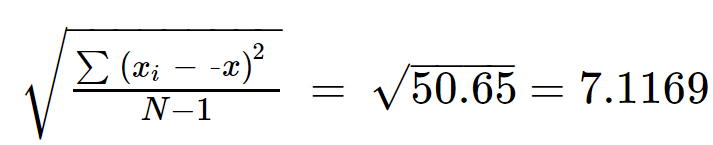
초 = 7.1169
위의 샘플 표준편차 계산기를 사용하여 이 예의 결과를 확인할 수 있습니다.
예 2 : 인구 표준 편차
주어진 모집단 데이터의 표준편차를 구합니다:
10, 12, 18, 14, 21, 27
해결책
1 단계: 인구 데이터의 기대값을 계산합니다.
N = 6
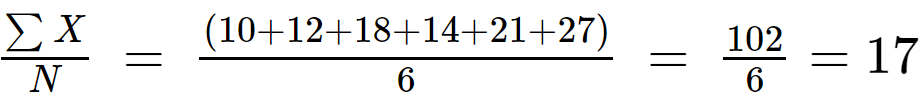
2 단계: 계산하다(x 나 - μ) 데이터 세트의 각 값에서 평균값을 빼고 차이의 제곱을 계산하여 양수로 만듭니다.
| 데이터 값 (x 나 ) | 엑스 나 - &마이크로; | (엑스 나 - 중) 2 |
| 10 | 10 - 17 = -7 | (-7) 2 = 49 |
| 12 | 12 - 17 = -5 | (-5) 2 = 25 |
| 18 | 18 - 17 = 1 | (1) 2 = 1 |
| 14 | 14 - 17 = -3 | (-삼) 2 = 9 |
| 21 | 21 - 17 = 4 | (4) 2 = 16 |
| 27 | 27 - 17 = 10 | (10) 2 = 100 |
3단계: (x에 대한 모든 값의 합을 구합니다. 나 - ) 2 .
=(x 나 - ) 2 = 49 + 25 + 1 + 9 + 16 + 100
=(x 나 - ) 2 = 200
4단계: 나누기 =(x 나 - ) 2 (N)으로.
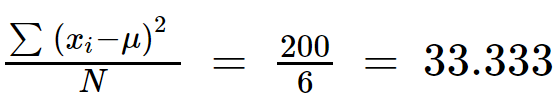
분산 = 33.333
Step 5: \(x)의 제곱근을 구합니다. 나 - ) 2 /N은 표준편차를 구합니다.
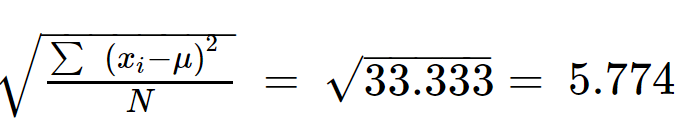
S = 5.774
위의 모집단 표준 편차 계산기를 사용하여 SD 계산 값을 교차 확인하십시오.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
다운로드
