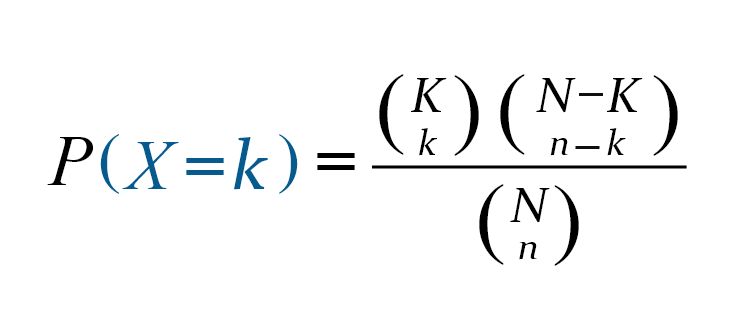Blog Worksheets Examples Practice Problems FAQs

Hypergeometric Distribution Calculator

How to use the hypergeometric distribution calculator?

Follow the steps below to utilize the hypergeometric distribution calculator:

Select the compute type.
Put the population size (N).
Put the number of success states in the population (K).
Put the sample size (n).
Put the number of success states in the sample (k).
Hit the "Calculate" button to compute the input
To enter new values click on the "Reset" button

Hypergeometric distribution calculator is a tool that is used to compute the mean, standard deviation, and variance of the entered data rendering the properties of Hypergeometric distribution.

What is hypergeometric distribution?

A hypergeometric distribution, which simulates success rates in a random sample taken from a limited population without replacement, is a probability distribution. It makes the supposition that there are two different kinds of objects in the population: successes and failures.,

The formula of hypergeometric distribution:

We can calculate the hypergeometric distribution by the following formula:

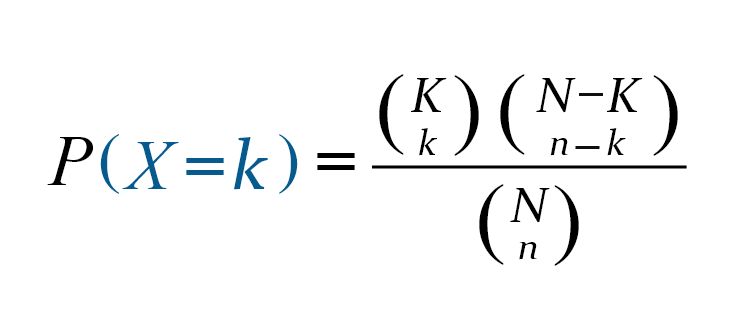
Hypergeometric distribution formula

N stands for Population size
K stands for the number of successful states in population.
(K) Number of success states in the sample.
n stands for sample size.

How to calculate the value of hypergeometric distribution?

Below example will help you to learn how to calculate the value of a hypergeometric distribution.

Example

Compute the value of hypergeometric distribution when N = 44, K = 22, n = 7, and k = 5.

Solution:

First, we find the mean

Step 1:

Mean = µ = n × (K / N)

µ = 7 (22 / 44)
µ = 7 × 0.5

µ = 3.5

Step 2:

Now we compute the variance
σ² = {n × (K / N)} {(N - K) / N} × {(N - n) / (N - 1)}

σ²= 7× (22 / 44) / × (44−22 / 44) × (44−7/ 44 -1)

σ² = 7 × 0.5 × 0.5 × 0.8605

σ² = 1.5058

Step 3:

To Compute the standard deviation, we take the square root of the variance.

√σ² =√ 1.5058

σ = 1.2271

Step 4:

Compute the probability

P (X = k)

P (X = 5) = 0.1587

P (X ≥ k):

P (X ≥ 5) = 0.206

P (X > k):

P (X > 5) = 0.0473

P (X ≤ k):

P (X > 5) = 0.9527

P (X < k):

P (X < 5) = 0.794

Hypergeometric Distribution Calculator

How to use the hypergeometric distribution calculator?

What is hypergeometric distribution?

The formula of hypergeometric distribution:

How to calculate the value of hypergeometric distribution?

Recent Blogs

Related Tools