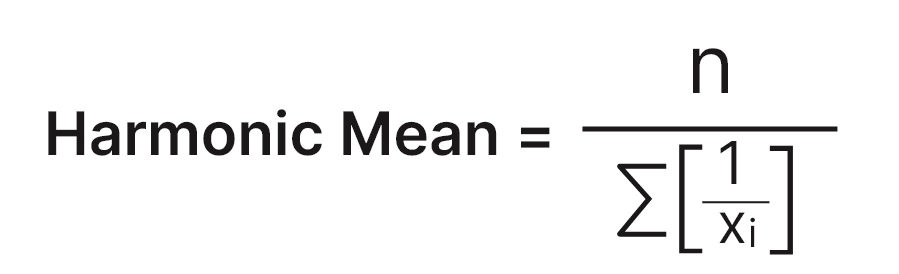Blog Worksheets Examples Practice Problems FAQs

Harmonic Mean Calculator

How to use the Harmonic mean calculator?

Follow the below steps to evaluate the harmonic mean using this calculator

Enter comma-separated values in the input box
Click on the “calculate” button
To erase all inputs hit the “reset” button.

What is harmonic mean in statistics?

The harmonic mean is one of the several types of “mean”. It is the reciprocal of the arithmetic mean. To calculate it we usually divide the sum of the reciprocals of all values by the total number of terms.

Formula of Harmonic mean:

Generally, for the ungroup data we use the following formula:

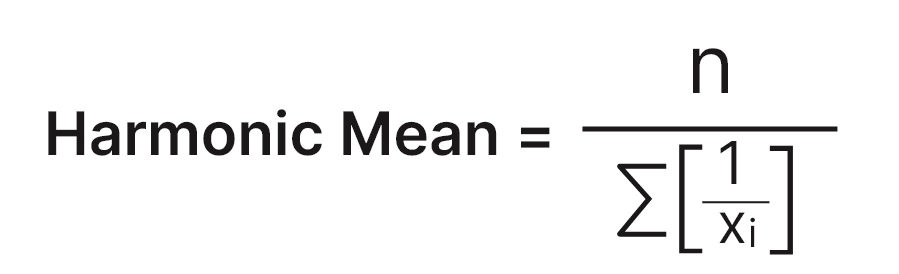
Harmonic mean formula

In the above formula:

“Σ (1 / X_i)” is the sum of reciprocals of all values
“n” is the total number of terms

How to Calculate Harmonic Mean?

Below examples are solved to calculate the harmonic mean of any ungroup data.

Example 1:

Evaluate the harmonic mean of the following data:

1, 5, 7, 3, 9, 12, 13

Solution:

Step 1: Extract the data

Let X = 1, 5, 7, 3, 9, 12, 13

Total number of terms = n = 7

Step 2: Put the values in the formula.

Harmonic mean = n / Σ (1 / X_i)

Harmonic mean = 7 / (1 / 1 + 1 / 5 + 1 / 7 + 1 / 3 + 1 / 9 + 1 / 12 + 1 / 13)

Harmonic mean = 7 / (1 + 0.2 + 0.1429 + 0.3333 + 0.1111 + 0.0833 + 0.0769)

Harmonic mean = 7 / 1.9475

Harmonic mean = 3.59424

Example 2:

If a person is driving a car at the rate of 50 km/h during the first 30 kilometers, 60 km/h during the 2^nd 30 kilometers, 90km/h during the 3^rd 30 kilometers, and 100km/h during the 4^th 30 kilometers calculate the average speed of the car.

Solution:

Step 1: Extract the data

Let,

Speed of car = X = 50, 60, 90, 100

Total number of terms = n = 4

Step 2: Put the values in the formula.

Harmonic mean = n / Σ (1 / X_i)

Harmonic mean = 4 / (1 / 50 + 1 / 60 + 1 / 90 + 1 / 100)

Harmonic mean = 4 / (0.02 + 0.0167 + 0.0111 + 0.01)

Harmonic mean = 4 / 0.0578

Harmonic mean = 69.23077

Harmonic Mean Calculator

How to use the Harmonic mean calculator?

What is harmonic mean in statistics?

Formula of Harmonic mean:

How to Calculate Harmonic Mean?

Recent Blogs

Related Tools