Blog Worksheets Examples Practice Problems FAQs

Five Number Summary Calculator

Enter the comma-separated values to generate 5 number summary using 5 number summary calculator

Why do we use five number summary calculator?

A five-number summary calculator is a tool used to summarize a set of data by computing five key statistics:

Minimum value
First quartile (Q1)
Median (Q2)
Third quartile (Q3)
Maximum value

What is a Five-Number Summary?

A five-number summary is a set of descriptive statistics that summarizes the distribution of a dataset. The five statistics that comprise the summary are the minimum value, the first quartile (Q1), the median, the third quartile (Q3), and the maximum value.

Table for a five-number summary:

Value	Description
Minimum	The minimum value is the smallest value in the dataset.
Q1	The first quartile (Q1) is the value that separates the lowest 25% of the data from the highest 75% of the data.
M (Median)	The median is the value that separates the lowest 50% of the data from the highest 50% of the data.
Q3	The third quartile (Q3) is the value that separates the lowest 75% of the data from the highest 25% of the data.
Maximum	The maximum value is the most significant value in the dataset.

The five-number summary can be used to create a box-and-whisker plot, which is a graphical representation of the distribution of the data. The plot consists of a box that represents the interquartile range (IQR) and whiskers that extend to the minimum and maximum values.

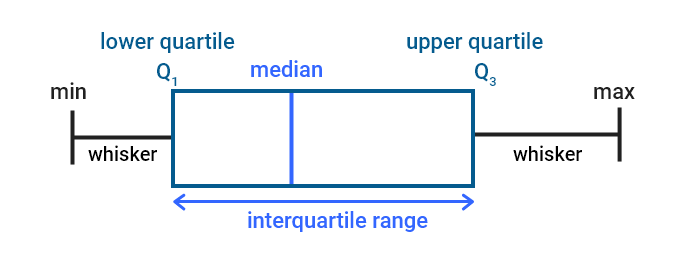
Box and a whisker plot of Five number summary

In the above picture box,

The plot spans the range between the first and third quartiles (Q1 and Q3).
The median is represented by a line inside the box.
The length of the box represents the spread of the middle 50% of the data, while the whiskers represent the range of the data outside of the box.

How to Calculate the Five-Number Summary by hand?

Calculating the by hand or with a calculator. Here are the steps to follow:

Sort the data in ascending order.
Calculate the median (M) of the dataset.
Divide the dataset into lower and upper halves; exclude the median from both if odd number of values.
Calculate the median of the lower half of the dataset. This is the first quartile (Q1).
Calculate the median of the upper half of the dataset. This is the third quartile (Q3).
The minimum value is the smallest value in the dataset.
The maximum value is the largest value in the dataset.

Example:

Suppose we have the following dataset: 5, 2, 7, 11, 9, 12, 18, 15, 21.

Arrange the data in ascending order: 2, 5, 7, 9, 11, 12, 15, 18, 21.
Calculate the median: 11.
Divide the dataset into two halves:
- Lower half: 2, 5, 7, 9.
- Upper half: 12, 15, 18, 21.
Calculate Q1: As the middle is odd then the median will be the average of two middle values (5+7)/2 = 6, so Q1 = 6.
Calculate Q3: The median of the upper half is (15+18)/2 = 16.5, so Q3 = 16.5.
The minimum value is 2.
The maximum value is 21.

Therefore, the five-number summary for this dataset is:

Min	Q1	M	Q3	Max
2	6	11	16.5	21

References:

Interquartile Range (IQR)| Statistics By Jim.
visualizing the box and whisker plot | statcan