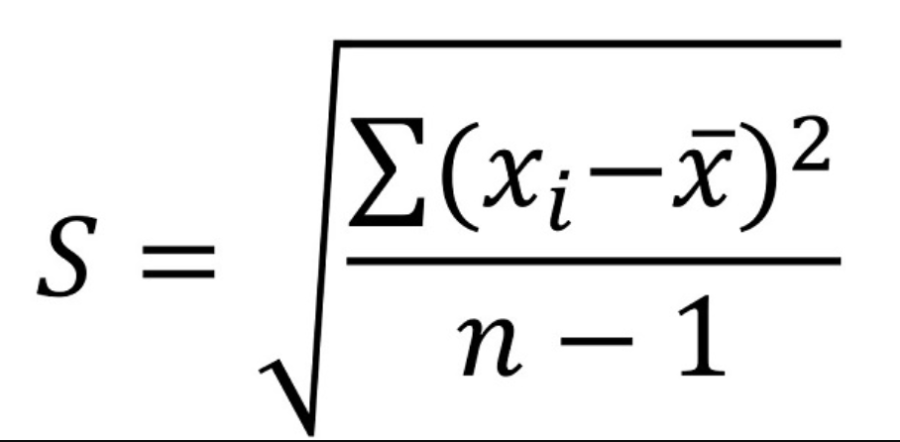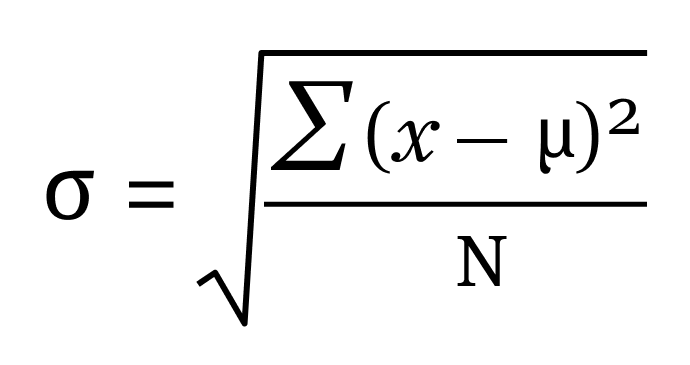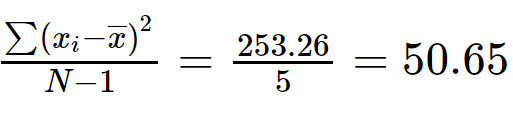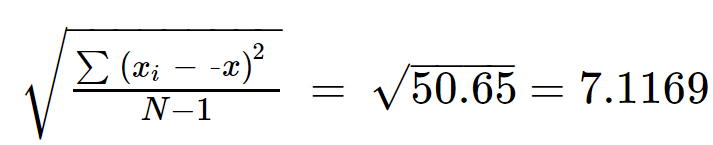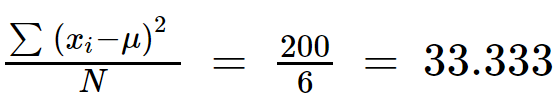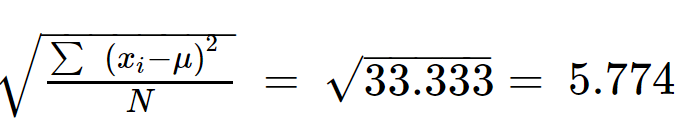Exploremos algunos puntos clave, como la definición de la desviación estándar, cómo encontrar la desviación estándar sin usar una calculadora de desviación estándar relativa y la ecuación de desviación estándar.
¿Cuál es la desviación estándar?
Una medida del grado en que los números están dispersos.
La desviación estándar es una estadística que mide la dispersión de un conjunto de datos en relación con su media y se calcula como la raíz cuadrada de la varianza. Se denota con el símbolo griego sigma σ.
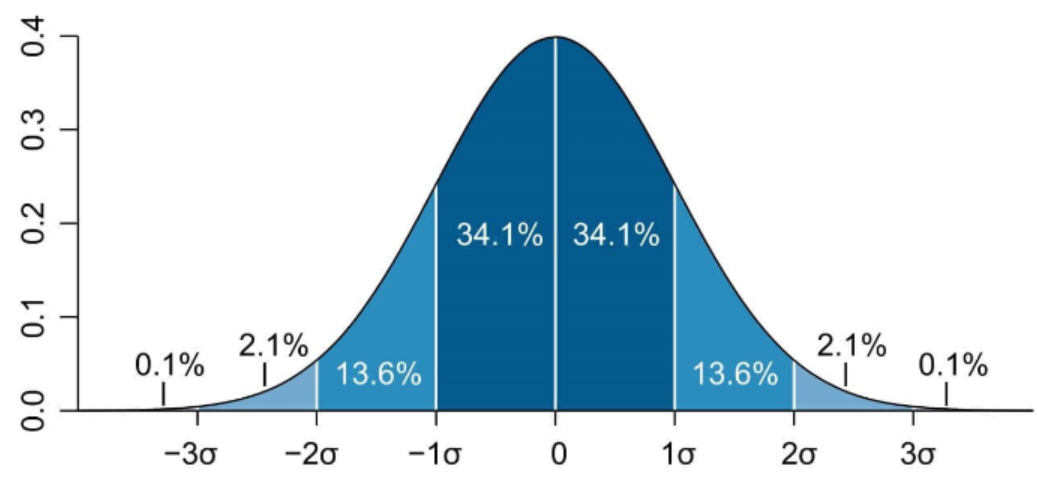
A continuación, puede encontrar el gráfico de una distribución normal con un ancho de 1 banda.
Fórmula de desviación estándar
La fórmula de la desviación estándar se puede expresar tomando la raíz cuadrada de la varianza.
Ejemplo de fórmula de desviación estándar
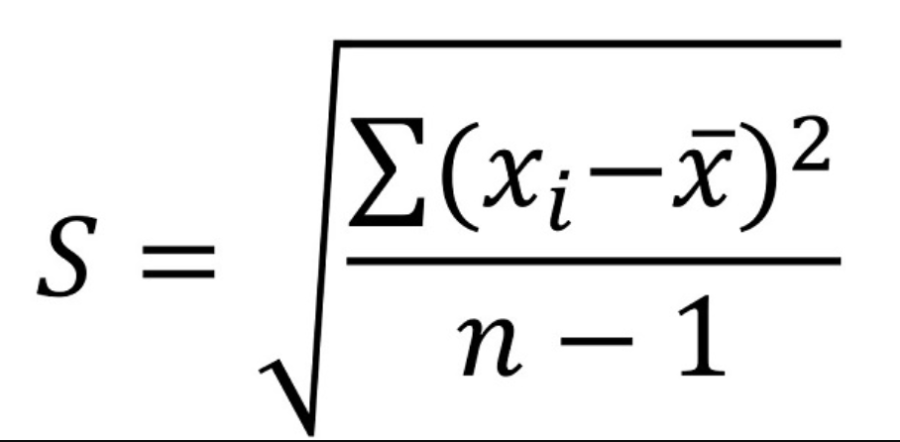
- s se refiere a la desviación estándar de la muestra
- norte es el número de observaciones
- X i son los valores observados del elemento de muestra, y
- X es el valor medio de la muestra
Fórmula de desviación estándar de la población
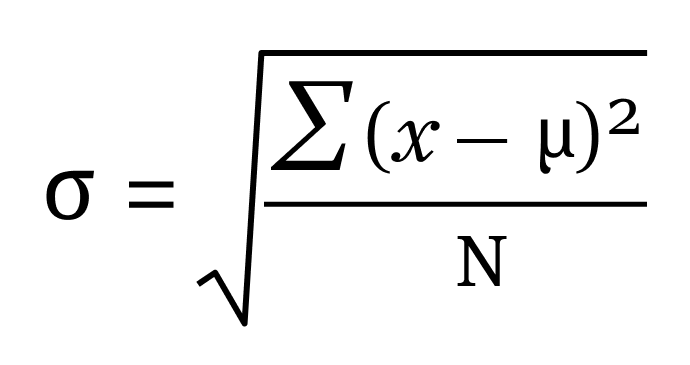
- σ se refiere a la desviación estándar de la población
- norte es el tamaño de la población
- X i son los valores observados de la población, y
- μ es la media poblacional
¿Cómo calcular la desviación estándar?
Cálculo de la desviación estándar se puede realizar utilizando la calculadora de media y desviación estándar anterior. Sin embargo, explicaremos el método para calcular SD con ejemplos.
Ejemplo 1: para la desviación estándar de la muestra
Encuentre la desviación estándar de la muestra dada:
30, 20, 28, 24, 11, 17
Solución
Paso 1: Calcula el significar valor de los datos de muestra:
N = 6
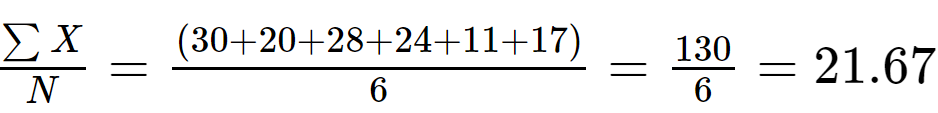
Paso 2: Calcular (x i - x̄) restando el valor medio de cada valor del conjunto de datos y calculando el cuadrado de las diferencias para hacerlos positivos.
| Valores de datos (x i ) | X i - x̅ | (X i - X ) 2 |
| 30 | 30 - 21,67 = 8,33 | (8.332) 2 = 69,4 |
| 20 | 20 - 21,67 = -1,67 | (-1.672) 2 = 2,78 |
| 28 | 28 - 21,67 = 6,33 | (6.332) 2 = 40 |
| 24 | 24 - 21,67 = 2,33 | (2.332) 2 = 5,43 |
| 11 | 11 - 21,67 = -10,67 | (-10.672) 2 = 113,85 |
| 17 | 17-11.67 = -4.67 | (-4.672) 2 = 21,80 |
Paso 3: Obtenga la suma de todos los valores para (x i - X) 2 .
∑(x i - X) 2 = 69.4 + 2.78 + 40 + 5.43 + 113.85 + 21.80
∑(x i - X) 2 = 253,26
Etapa 4: Dividir ∑(x i - X) 2 con (N-1).
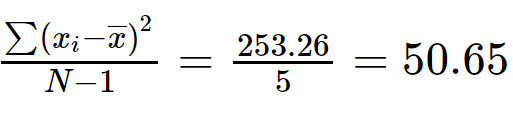
Varianza = 50,65
Paso 5: Saque la raíz cuadrada de ∑(x i - X) 2 /(N-1) para obtener la desviación estándar.
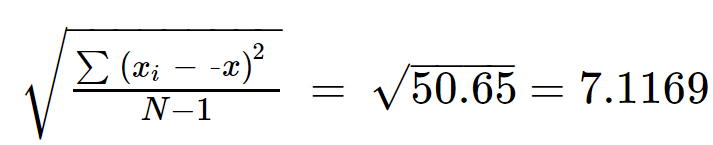
s = 7,1169
La calculadora de desviación estándar de muestra anterior se puede utilizar para verificar el resultado de este ejemplo.
Ejemplo 2: para población Desviación Estándar
Encuentre la desviación estándar de los datos de población dados:
10, 12, 18, 14, 21, 27
Solución
Paso 1: Calcule el valor esperado de los datos de población:
norte = 6
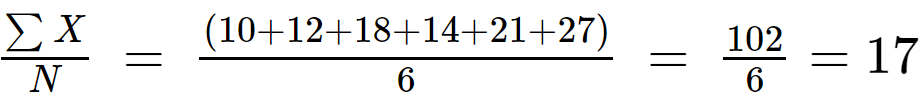
Paso 2: Calcular (x i - µ) restando el valor medio de cada valor del conjunto de datos y calculando el cuadrado de las diferencias para hacerlos positivos.
| Valores de datos (x i ) | X i -µ | (X i -µ) 2 |
| 10 | 10-17 = -7 | (-7) 2 = 49 |
| 12 | 12 - 17 = -5 | (-5) 2 = 25 |
| 18 | 18 - 17 = 1 | (1) 2 = 1 |
| 14 | 14 - 17 = -3 | (-3) 2 = 9 |
| 21 | 21 - 17 = 4 | (4) 2 = 16 |
| 27 | 27 - 17 = 10 | (10) 2 = 100 |
Paso 3: Obtenga la suma de todos los valores para (x i -µ) 2 .
∑(x i -µ) 2 = 49 + 25 + 1 + 9 + 16 + 100
∑(x i -µ) 2 = 200
Etapa 4: Dividir ∑ (x i -µ) 2 con (N).
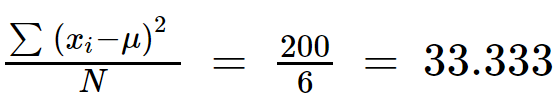
Varianza = 33.333
Paso 5: Saque la raíz cuadrada de ∑(x i -µ) 2 /N para obtener la desviación estándar.
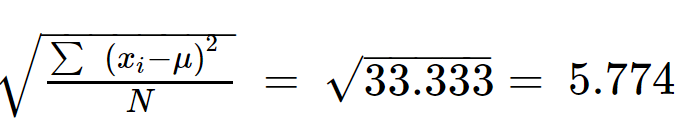
σ = 5.774
Utilice la calculadora de desviación estándar de población anterior para verificar los valores para los cálculos de DE.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
