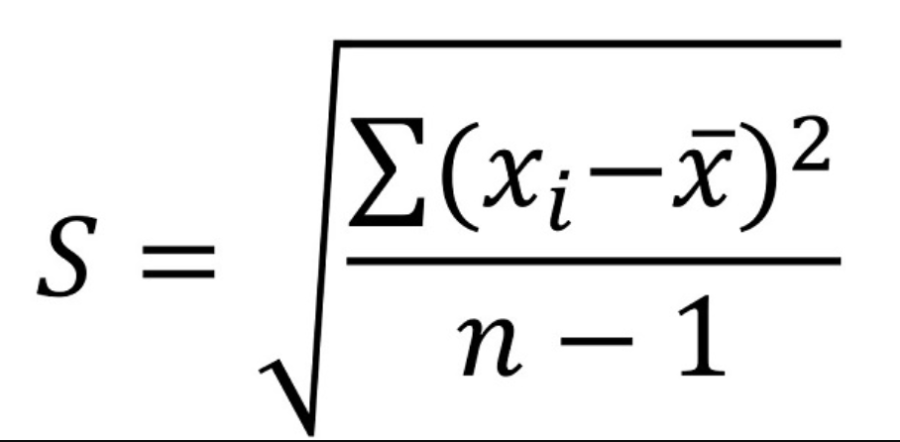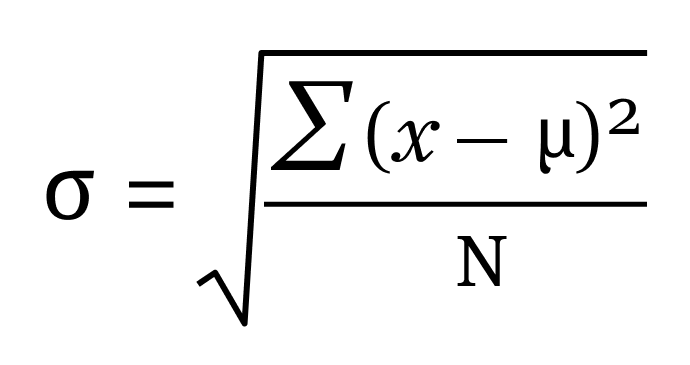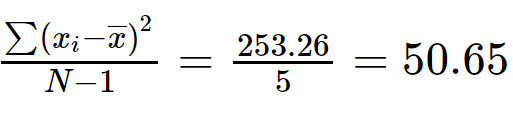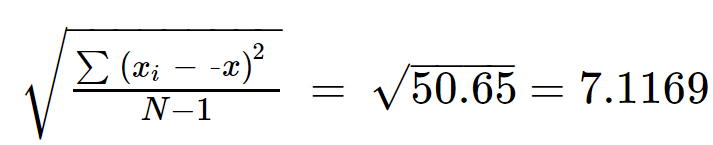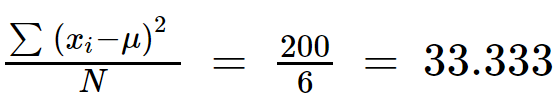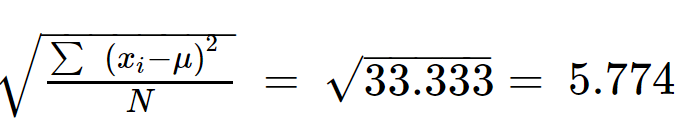Lassen Sie uns einige wichtige Punkte untersuchen, z. B. die Definition der Standardabweichung, die Ermittlung der Standardabweichung ohne Verwendung eines relativen Standardabweichung rechner und die Standardabweichung gleichung.
Was ist Standardabweichung?
Ein Maß dafür, wie weit die Zahlen verteilt sind.
Die Standardabweichung ist eine Statistik, die die Streuung eines Datensatzes relativ zu seinem Mittelwert misst und als Quadratwurzel der Varianz berechnet wird. Es wird mit dem griechischen Symbol Sigma σ bezeichnet.
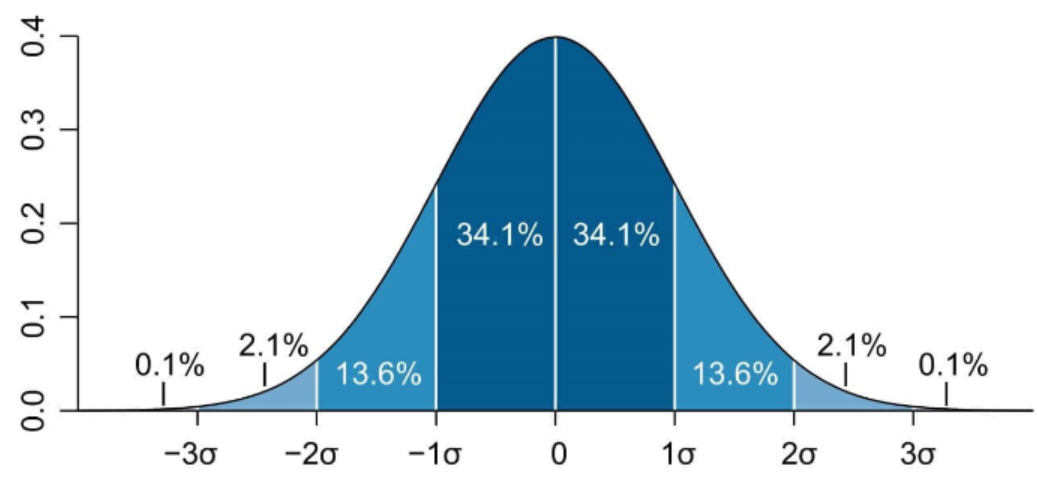
Unten finden Sie das Diagramm einer Normalverteilung mit einer Breite von 1 Band.
Standardabweichung formel
Die Standardabweichung formel kann ausgedrückt werden, indem die quadratische Wurzel des Varianz .
Beispiel formel Standardabweichung
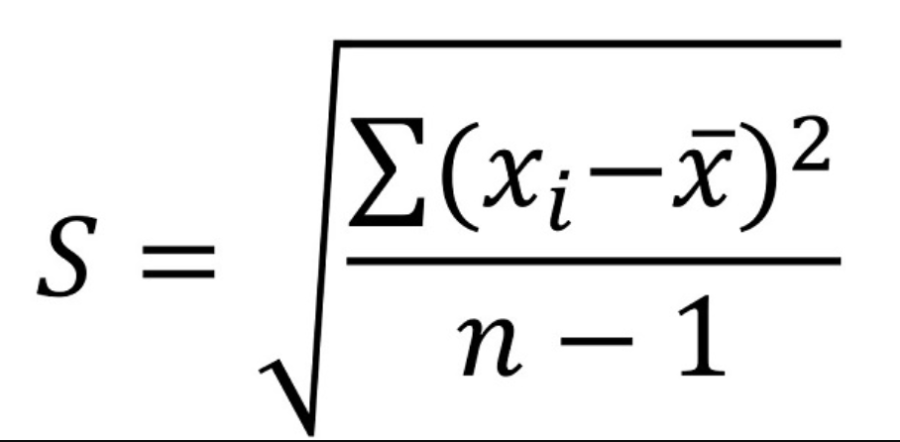
- S bezieht sich auf Probenstandardabweichung
- N ist die Anzahl der Beobachtungen
- X ich sind die beobachteten Werte des Beispielelements und
- X ist der Mittelwert der Stichprobe
Formel Standardabweichung Grundgesamtheit
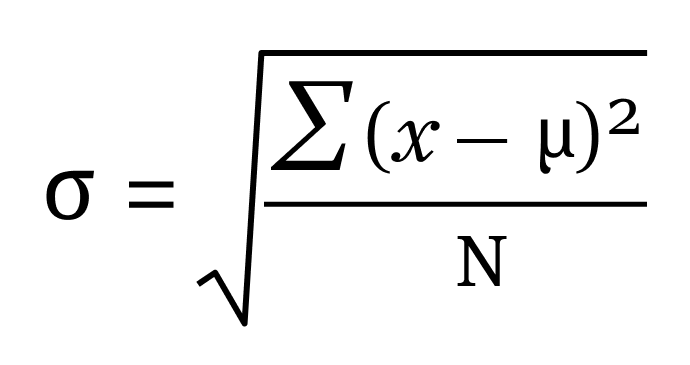
- σ bezieht sich auf die Populationsstandardabweichung
- N ist die Größe der Bevölkerung
- X ich sind die beobachteten Werte der Grundgesamtheit und
- μ ist der Bevölkerungsmittelwert
Wie standardabweichung berechnen?
Berechnung Standardabweichung kann mit dem Mittelwert- und Standardabweichungsrechner oben durchgeführt werden. Wir erläutern jedoch die Methode zur Berechnung der SD anhand von Beispielen.
Beispiel 1: Für Stichproben standardabweichung
Ermitteln Sie die Standardabweichung der gegebenen Stichprobe:
30, 20, 28, 24, 11, 17
Lösung
Schritt 1: Berechne das bedeuten Wert der Beispieldaten:
N = 6
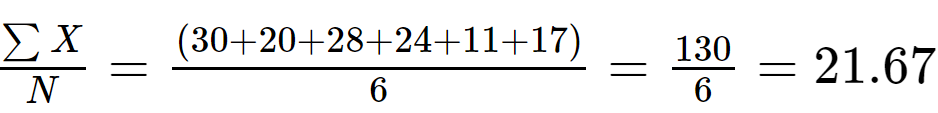
Schritt 2: Berechnen Sie (x ich - x̄) durch Subtrahieren des Mittelwerts von jedem Wert des Datensatzes und Berechnen des Quadrats der Differenzen, um sie positiv zu machen.
| Datenwerte (x ich ) | X ich - x̅ | (X ich - X ) 2 |
| 30 | 30-11.67 = 8,33 | (8.332) 2 = 69,4 |
| 20 | 20 - 21,67 = -1,67 | (-1,672) 2 = 2,78 |
| 28 | 28 - 21,67 = 6,33 | (6.332) 2 = 40 |
| 24 | 24 - 21,67 = 2,33 | (2.332) 2 = 5,43 |
| 11 | 11 - 21,67 = -10,67 | (-10,672) 2 = 113,85 |
| 17 | 17 - 21,67 = -4,67 | (-4,672) 2 = 21,80 |
Schritt 3: Ermitteln Sie die Summe aller Werte für (x ich - X) 2 .
∑(x ich - X) 2 = 69,4 + 2,78 + 40 + 5,43 + 113,85 + 21,80
∑(x ich - X) 2 = 253,26
Schritt 4: Teilen Sie ∑(x ich - X) 2 mit (N-1).
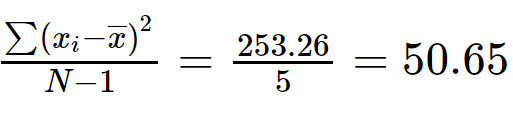
Varianz = 50,65
Schritt 5: Ziehen Sie die Quadratwurzel aus ∑(x ich - X) 2 /(N-1), um die Standardabweichung zu erhalten.
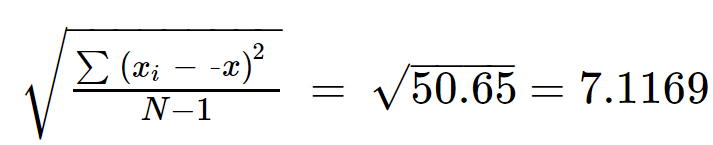
s = 7,1169
Der obige Beispiel -Standardabweichungsrechner kann verwendet werden, um das Ergebnis dieses Beispiels zu überprüfen.
Beispiel 2: Für Bevölkerung Standardabweichung
Ermitteln Sie die Standardabweichung der gegebenen Bevölkerungsdaten:
10, 12, 18, 14, 21, 27
Lösung
Schritt 1: Berechnen Sie den erwarteten Wert der Bevölkerungsdaten:
N = 6
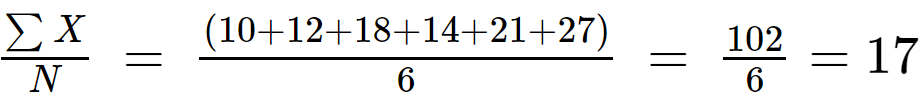
Schritt 2: Berechnen Sie (x ich - µ), indem Sie den Mittelwert von jedem Wert des Datensatzes subtrahieren und das Quadrat der Differenzen berechnen, um sie positiv zu machen.
| Datenwerte (x ich ) | X ich - µ | (X ich - µ) 2 |
| 10 | 10 - 17 = -7 | (-7) 2 = 49 |
| 12 | 12 - 17 = -5 | (-5) 2 = 25 |
| 18 | 18-17 = 1 | (1) 2 = 1 |
| 14 | 14 - 17 = -3 | (-3) 2 = 9 |
| 21 | 21 - 17 = 4 | (4) 2 = 16 |
| 27 | 27 - 17 = 10 | (10) 2 = 100 |
Schritt 3: Ermitteln Sie die Summe aller Werte für (x ich - M) 2 .
∑(x ich - M) 2 = 49 + 25 + 1 + 9 + 16 + 100
∑(x ich - µ) 2 = 200
Schritt 4: Teilen Sie ∑(x ich - µ) 2 mit (N).
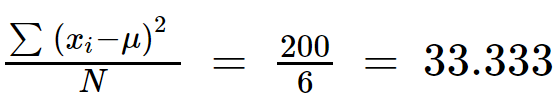
Varianz = 33,333
Schritt 5: Ziehen Sie die Quadratwurzel aus ∑(x ich - µ) 2 /N, um die Standardabweichung zu erhalten.
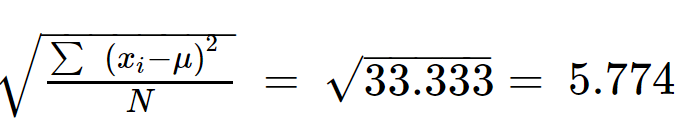
σ = 5,774
Verwenden Sie den obigen Rechner Standardabweichung der Grundgesamtheit, um die Werte für SD-Berechnungen gegenzuprüfen.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
